Je Pi polynom?

Video: Je Pi polynom?

2024 Autor: Lynn Donovan | [email protected]. Naposledy změněno: 2023-12-15 23:44

Pi (π) se nepovažuje za a polynom . Je to hodnota vztahující se k obvodu kruhu. Na druhou stranu, polynom se týká rovnice obsahující čtyři nebo více proměnných.

Může být pí součástí polynomu?

Odpověď je ne. Pokud tam byl a polynom s algebraickými koeficienty by také existoval a polynom s racionálním koeficientem (s větším stupněm). To proto, že ˉQ je algebraicky uzavřené. Předpokládejme, že π byly kořenem a polynom f(x)=xn+an−1xn−1+⋯+a0, přičemž ai jsou algebraická čísla.

Za druhé, co tvoří polynom? V matematice a polynom je výraz skládající se z proměnných (také nazývaných neurčité) a koeficientů, který zahrnuje pouze operace sčítání, odčítání, násobení a nezáporné celočíselné exponenty proměnných. Příklad a polynom z jedné neurčité, x, je x² − 4x + 7.

Je Pi v tomto ohledu mononomní?

Ano, π π je a monomiální protože je to číslo.

Musí mít polynom proměnnou?

Takže: A polynom umět mít konstanty, proměnné a exponenty, ale nikdy dělení a variabilní . Také mohou mít jeden nebo více termínů, ale ne nekonečný počet termínů.

Doporučuje:

Jak se nazývá polynom se 6 členy?

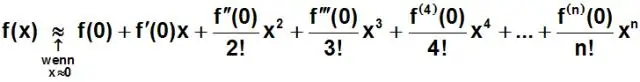
Následující názvy jsou polynomům přiřazeny podle jejich stupně: Stupeň 4 – kvartický (nebo, pokud mají všechny termíny sudý stupeň, bikvadratický) Stupeň 5 – kvintický. Stupeň 6 – sextický (nebo méně často hexický)

Co je to polynom prvního stupně?

Polynomy prvního stupně. Polynomy prvního stupně jsou také známé jako lineární polynomy. Zejména polynomy prvního stupně jsou čáry, které nejsou ani vodorovné, ani svislé. Častěji se jako koeficient x místo a používá písmeno m a používá se k vyjádření sklonu čáry